Concluding Remarks Hamiltonian Dynamics of Higher Order Hamiltonian

The stability analysis

First of all we remark that the second order Hamiltonian (34) is equivalent, by a canonical transformation, to the sum of two coupling harmonic oscillators having energies of opposite signs

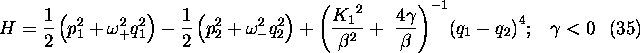
where

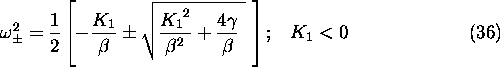
This system has indefinite energy, but can be stable as was demonstrated in [15]. The important feature here is that the coupling is divergent at the transition line given by [11]

 

Thus to obtain correct results according to experimental data near the transition line, this theory must be renormalized. A suitable renormalization may describes the reentrant phenomenon in the - C line boundary observed in [8].

The qualitative behavior of the non-linear system may be obtained from the linearized system at the equilibrium point , far from the transition line, that is for

or

The Taylor expansion of (34) at up second order, gives the Hamiltonian

The linearized Hamilton's equation are

and the matrix corresponding the Hamiltonian vector field is:

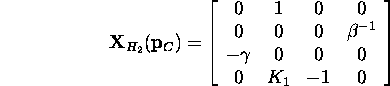
The stability condition for is given by

that is,

The eigenvalues of are obtained from characteristic polynomial

whose roots are

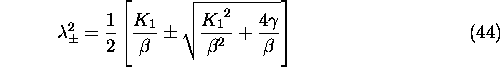
Thus, far from the transition line, the solution of the linearized system of differential equation is just a helix

with frequency

for

and

for

Finally at the solution is also an helix with frequency given by