Next: The stability analysis Up: Hamiltonian Dynamics of Previous: The stability analysis
Next: The
stability analysis Up: Hamiltonian
Dynamics of Previous: The
stability analysis
We show here that higher order derivative Hamiltonian theory may by applied to systems described by one dimensional free energy density
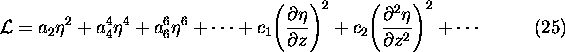
as is the case of ferroelectric liquid crystals [11].
Lagrangian theories with higher order derivatives in the evolution parameter,
occurs in many different areas of physics, like for example general relativity,
non-linear 
- models, string theories and Dirac's model of the radiating electron and
has been a subject of increasing research. Detailed exposition of the higher
order theory, can be found in [12, 13].
The Hamiltonian theory corresponding to a non-degenerated higher - order Lagrangian, was formulated by Ostrogradski [14] in the middle of the last century. To be concise, we only sketch the basic formulas.
Let consider an one dimensional system described by a Lagrangian of order Q
here, 
means the derivative of order i in the evolution parameter
The Euler - Lagrange equations are written as
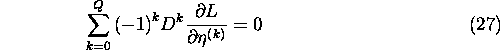
and the canonical momenta is defined by
If
the elimination of 
in (28), gives the phase space coordinates
The higher order Hamiltonian is obtained from the Legendre transformation,
This Hamiltonian generates motions, governed by the generalized Hamilton's equations
How it is well known the C - 
transition in ferroelectric liquid crystals, near the Lifshitz point, is
described by the free energy functional [11]
where
and
The function 
is a second - order Lagrangian function defined in 
where Q is an one - dimensional configuration space.
Here the elastic term 
, may be positive, negative or null, due to the presence of 
.
The condition 
, that is
defines the second order line between A - C phases, with 
.
For 
the equilibrium point is in the disordered A phase, at 
. For 
the equilibrium point is in the ordered - C phase, at 
. If 
with
, there is a 
transition of the equilibrium point of C to a periodic solution, of the
phase.
Using (28) we obtain the canonical momenta
By the Legendre transformation, we obtain the second order Hamiltonian,
with coordinates 
The Hamiltonian (34), gives rise the following system of differential equations
