Next: The stability analysis Up: Hamiltonian Dynamics of Previous: Introduction
Next: The
stability analysis Up: Hamiltonian
Dynamics of Previous: Introduction
The A - 
phase transitions is described by the free energy
with
where, the coefficient A , depends linearly on temperature :
; 
is the diamagnetic anisotropy and K is the elastic modulus [8].
The function 
, is a Lagrangian function. Indeed, it is a function defined in the tangent
space TQ of a 2 - dimensional configuration space, Q, with
local coordinates 
, parameterized by z.
The coefficient K must be positive in order to give a consistent Lagrangian theory. If K<0 the theory lacks a lower - energy bound. The Lifshitz point, is induced by a change of sign of K. In the impossibility to have K<0 the Lifshitz point is realized by the Lifshitz function
where 
is a constant. The Lagrangian system defined by (2),
is a regular Lagrangian system that is
Thus by the usual Legendre transformation
we obtain the Hamiltonian
where
and
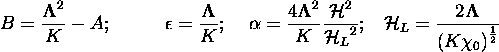
The non-linear Hamiltonian system defined by (6) is non-integrable, and belongs to a class of two dimensional Hamiltonian systems that possess transversal intersecting stable and unstable manifold that leads to homoclinic chaos [10].
When 
, the system is completely integrable with 
, as the second constant of motion besides the energy. This may be verified
by direct calculation of the Poisson bracket 
.
In order to study the quasi-periodic solutions of such system, we have analyzed the Poincaré section of the nearly two - tori defined by H and F in the phase space.
The Hamiltonian (6), gives rise the following system of differential equations
where 
.
The linearized system around the equilibrium point 
is
where
is the Taylor expansion of (6) around 
up to second order. (Here we have retained the same variables 
as for the non-linear system). It is worth to stress that is sufficient
to consider the linear Hamiltonian (7) in order
to obtain the qualitative behavior of the system, when it is represented
by non-linear Hamiltonian (6). Figure
1a (linear case) and figure 1b (non-linear
case) represent the Poincaré sections of the system, which show
a similar behavior as we have mentioned above. The Poincaré section,in
both cases, was calculated by using the same parameter set.
