Return to Main-Page

DETERMINAÇÃO DE HIPERSUPERFÍCIES DE ENERGIA PARA

SISTEMAS TRIATÔMICOS USANDO O MÉTODO

“GENERALIZED SIMULATED ANNEALING”.

Curt Max de Ávila Panisset   e    Kleber Carlos Mundim

Instituto de Química – Universidade de Brasília

kcmundim@unb.br

ÍNDICE:

1. ICAPÍTULO 1   Introdução 5
2. CAPÍTULO 2 6 Estudo e descrição de sistemas moleculares. 6

2.1. A aproximação de Born-Oppenheimer

2.2. A Superfície de Energia Potencial (SEP)

2.3. Métodos de ajuste e funções analíticas a serem usadas

2.3.1. Método de ajuste por Splines

2.3.2. Métodos em que potenciais semi-empíricos são ajustados 

                ou corrigidos para reproduzir dados experimentais ou ab-initio

2.3.3. Ajustes empíricos baseados em desenvolvimento de múltiplos corpos.

2.3.4. Polinômios em coordenadas físicas

2.3.5. Polinômios no espaço Bond Order

3. CAPÍTULO 3 23 A otimização do potencial por meio do Generalized Simulated Annealing. 23

3.1. Simulação por termalização ou Simulated Annealing (SA)

3.2. O General Simulated Annealing (GSA)

3.3. Ajustes propostos e algoritmo utilizado

4. CAPÍTULO 4 40 Determinando a SEP: otimização do potencial por meio do GSA 40

4.1. Aplicação do GSA no caso específico de ajuste de SEP’s

4.2. Resultados obtidos

4.3. Interpretação dos resultados obtidos

5. CAPÍTULO 5 45     Conclusões 
6. BIBLIOGRAFIA 48

ABSTRACT:

Using the optimization method Generalized Simulated Annealing (GSA) an analytical function was fitted into the hyper-potential energy surface (PES) of the H₃⁺ molecule. To do this task, a set of ab initio energies considering several nuclear configurations were used from available literature. Handling this surface it was possible to determine dynamic properties such as vibrational energies. It is well known that through a PES one is able to study the nuclear movements of a molecule.

            The results obtained by the usage of this new methodology are compatible with the best ones known in literature. It was also shown that the GSA method is efficient to map a PES.

RESUMO:

Fazendo-se uso do método Generalized Simulated Annealing (GSA), ajustou-se para uma função analítica, superfície de energia potencial (SEP), um conjunto de energias, para várias configurações nucleares, calculados via métodos ab-initio para a molécula de H₃⁺. Esta superfície foi usada na descrição das propriedades dinâmicas, como propriedades vibracionais. Sabe-se que o conhecimento da SEP permite estudar os movimentos nucleares numa dinâmica molecular.

            Mostrou-se que os resultados obtidos, nesta nova metodologia, são compatíveis com aqueles conhecidos na literatura. Mostrou-se também a viabilidade e eficiência do método GSA no mapeamento da hipersuperfície de energia potencial.

CAPÍTULO 1

Introdução

Químicos e Físicos, assim como outros cientistas, têm dedicado seu tempo buscando entender o universo, aprendendo e descobrindo seus princípios e fundamentos para poder prever o comportamento de diversos sistemas e fenômenos, ou para aprimorar a tecnologia e melhorar o nível de vida em geral.

Na química, um grupo de sistemas de particular interesse é o que compreende o universo atômico e molecular, afinal a compreensão do comportamento dos átomos e moléculas é a essência de tal ciência. Têm se concentrado esforços os mais diversos para a descrição destes sistemas particulares.

Tais universos de estudo são descritos, de acordo com a teoria quântica, por meio da equação de Schrödinger. Contudo esta equação não pode ser resolvida em sua forma dependente do tempo para sistemas de muitos corpos e por isso propriedades dinâmicas não podem ser descritas. Faz-se mister buscar metodologias alternativas para contornar esta limitação.

Neste contexto, o principal objetivo do presente trabalho é o de propor uma metodologia alternativa para a obtenção de propriedades dinâmicas de moléculas, sem resolver, diretamente, a equação de Schrödinger, dependente do tempo diretamente. Nesta metodologia, calculam-se as energias eletrônicas para diversas configurações atômicas, usando a equação de Schrödinger independente do tempo, e em seguida constrói-se a função energia potencial, a qual é conhecida como uma hiper-superfície de energia potencial (SEP). A SEP é a função que governa a dinâmica dos núcleos atômicos.

Com esta função, a SEP, em mãos, pode-se calcular como os núcleos vão se comportar neste potencial e prever como eles se comportarão ao longo do tempo, ou seja, possibilitando a obtenção de informações muito interessantes como, por exemplo, valores do espectro vibracional.

A SEP é muito sensível e sua obtenção é um procedimento muito delicado e por isso as configurações dos átomos envolvidos no sistema devem ser muito bem escolhidas e os cálculos realizados devem ser de extrema precisão.

O íon H₃⁺ foi escolhido para testar tal metodologia. Sua escolha se baseia no fato de ser um sistema simplificado, permitindo que suas energias sejam calculadas com altíssimo grau de refinamento, sem acarretar excessivo esforço computacional. Este fato torna o H₃⁺ um ótimo candidato a testar a metodologia proposta. Vale ressaltar que o H₃⁺  é um sistema muito bem descrito na literatura, oferecendo uma vasta bibliografia, que vai de dados experimentais recentes aos mais modernos trabalhos em química e física computacionais que servem de referência e como parâmetro no julgamento do  resultado do método proposto.

CAPÍTULO 2

Estudo e descrição de sistemas moleculares

            O descobrimento da teoria quântica promoveu uma mudança de rota no desenvolvimento do conhecimento humano.  Em particular, os postulados de  Broglie e de Einstein, onde estavam expressas as idéias de quantização de energia e as propriedades ondulatórias da matéria, foram de suma importância na descrição da química moderna. Esses preceitos estão expressos pelas equações abaixo:

                                                                                             (2.1)

                                                                                             (2.2)

            Aqui o “h” representa a constante de Planck, “E” a energia, “” é a freqüência e “λ” o comprimento de uma onda eletromagnética.

            Deste ponto em diante apareceram também evidências experimentais de que os componentes de sistemas microscópicos (partículas) não se moviam de acordo com as leis da mecânica newtoniana. Portanto, uma partícula microscópica age, em determinadas situações, como se seu comportamento fosse governado por uma onda de  Broglie, ou uma função de onda.

Sendo assim, para cada sistema, pode-se afirmar que existe uma equação que controla as propriedades da função de onda, e por conseguinte, a relação entre esta função e o comportamento da partícula.

Com base nesses preceitos, Schrödinger propôs uma equação dinâmica, a qual ficou conhecida como equação de Schrödinger, que nada mais faz do que relacionar a energia cinética e potencial do sistema à energia total, usando-se a função de onda referente a um dado sistema. Em sua forma mais genérica ela pode ser expressa da seguinte forma:

                                                                                            (2.3)

Cuja forma independente do tempo é,

                                                                            (2.3a)

Onde “K” representa a função (ou operador) da energia cinética, “V” representa a expressão da energia potencial, “E” representa a energia total e “” é a função de onda do sistema. Se adotarmos a expressão de energia cinética como sendo igual ao resultado da divisão do quadrado do momento por duas vezes a massa (K=p²/(2m)),  a equação de Schrödinger deve ser escrita da seguinte forma:

                                         (2.4)

            A equação 2.4 é na verdade uma outra forma de se escrever a equação 2.3, contudo as energias estão expressas na forma de operadores que os representam. É importante lembrar que pelo fato de não ter sido usada a equação relativística para a energia cinética, a equação 2.4 não representa tal comportamento. Para que isso possa ser sanado basta usar como fórmula de energia cinética a fórmula abaixo:

                                                                            (2.5)

Embora as deduções tenham sido citadas, nenhuma delas é escopo deste trabalho, mas  podem ser acompanhadas em diversos livros textos [1].

Voltando novamente nossa atenção para a equação 2.4, percebe-se que a função de onda que lá aparece tem dependência das variáveis espaciais (x,y e z) e da variável temporal (t). Infelizmente, a solução desta equação diferencial é um árduo problema, mesmo para sistemas moleculares simples. Como temos de um lado a derivada temporal e de outro a espacial, poderia ser feita uma separação de variáveis, desde que a energia potencial não dependa explicitamente do tempo “t”, ou seja, ela  poderá ser escrita na forma de V(x,y,z).

Como na mecânica quântica,  na mecânica clássica, quase todos os sistemas têm energias potenciais, desta forma, a condição não é uma restrição séria. Infelizmente, no caso de interesse em determinar as propriedades dinâmicas de uma molécula, a energia potencial é dependente do tempo. Daí, um dilema: caso seja feita a separação de variáveis não se tem acesso às propriedades dinâmicas e se não for feito tal processo matemático não podemos resolver o sistema.

Não havendo outra saída, fez-se a separação de variáveis pretendendo, adiante, propor uma maneira para contornar o fato de que as soluções não contemplam a dependência do tempo.  Depois de feito o processo de separação de variáveis temos a função de onda da seguinte forma:

                                                                                    (2.6)

e a equação de Schrödinger pode ser reescrita assim:

                                             (2.7)

            É importante perceber que ψ não é uma função de onda e sim uma autofunção de Ψ (a real função de onda) e que a energia não é mais um operador e sim um autovalor referente ao sistema. Desta forma, pode-se representar a eq 2.7 em termos de um operador conhecido como Hamiltoniano, que encerra em si a parte referente às energias potencial e cinética. Sua representação matemática pode ser feita da seguinte forma:

                                                                                                    (2.8)

            Então, o interesse passa a ser a determinação das soluções aproximadas da equação de Schrödinger não relativística e independente do tempo para um sistema de núcleos e elétrons descrito pelos vetores de posição R_A e r_i, respectivamente. A distância entre o elétron “i” e o núcleo “A” é r_iA = Ir_iAI = Ir_i – R_AI; a distância entre dois elétrons “i” e “j” é r_ij = Ir_i – r_jI, e a distância entre dois núcleos “A” e “B” é R_AB = IR_A – R_BI.  O sistema que acabou de ser descrito pode ser visto na figura abaixo:

Figura 2.1 – Representação gráfica de um sistema com dois núcleos e dois elétrons (A e B representam núcleos e i e j elétrons)

Sendo assim, expresso em unidades atômicas, o Hamiltoniano para um sistema de N elétrons e M núcleos é [2]:

                             (2.9)

onde M_A é a razão de massa do núcleo “A” com relação a massa de um elétron, Z_A é o número atômico deste núcleo. Os operadores Laplacianos referem-se à diferenciação a respeito das coordenadas do ente (um determinado elétron ou núcleo) representado pelo seu subíndice. Nesta equação o primeiro termo refere-se à energia cinética dos elétrons, o segundo diz respeito à energia cinética dos núcleos, o terceiro descreve a atração entre os elétrons e núcleos, o quarto e quinto representam a repulsão entre os elétrons e entre os núcleos respectivamente.

Faremos agora, um breve parêntese para explicar o que venham a ser as coordenadas atômicas. Como pode ser visto na equação 2.7, diversas constantes e grandezas estão presentes, tornando a equação extensa, e por isso, foi convencionado usar as unidades atômicas para que tais constantes pudessem ser reduzidas à unidade. Deste modo, a unidade de massa passou a ser a massa do elétron (9,1095x10^-31Kg), bem como sua carga (1,6022x10^-19C), a distância passou a ser expressa em Bohr´s (5,2918x10^-11m), a energia em Hartrees (4,3598x10^-18j). Portanto, a equação de Schrödinger de um elétron em um potencial coulombiano que era representada por:

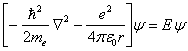                                                                       (2.10)

passa a ser representada por:

                                                                                  (2.11)

2.1 – A APROXIMAÇÃO DE BORN-OPPENHEIMER

Como foi visto anteriormente, fazendo-se a separação de variáveis e tornando a equação que descreve um sistema molecular independente do tempo, chega-se à  expressão dada na equação 2.9.

Mesmo assim a resolução de tal equação não é possível devido aos inúmeros acoplamentos elétrons-núcleo existentes no sistema. Então, são necessárias outras aproximações. Uma boa aproximação seria considerar que os elétrons em uma molécula movem-se em um campo onde os núcleos estão fixos.

Na verdade a real consideração que está sendo feita é que a massa dos núcleos é consideravelmente maior que a dos elétrons. Então, se estes estão se movendo, assim o fazem a uma velocidade muito menor que a dos elétrons, de tal forma que se pode considerar estarem os núcleos estacionários com relação aos elétrons. Essa aproximação é conhecia como aproximação adiabática.

Considerando uma expansão adiabática, pode-se escrever uma função eletrônica (f(r,R)) que varia vagarosamente com os valores de “R”, sendo “R” um parâmetro e para cada valor de R ter-se-á uma configuração correspondente para (f(r,R).

Faz-se novamente uma separação de variáveis e a função de onda que dependia simultaneamente de R e r passa a ser dividida em uma função que depende apenas das coordenadas dos elétrons (e que está parametrizada com relação às coordenadas dos núcleos) e de uma outra função que representa os núcleos. Então:

                                                          (2.12)

Substituindo a equação 2.12 e 2.9 na equação 2.8 obtêm-se:

                              (2.13)

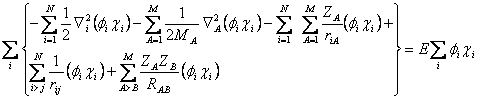
Escrevendo a equação 2.13 em sua forma mais extensa:

                     (2.14)

Contudo:

                            (2.15)

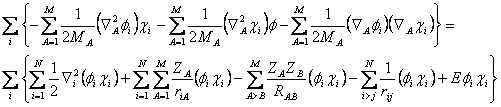
Substituindo 2.15 em 2.14 e isolando tal termo a seguinte expressão aparece:

                             (2.16)

Para cada valor de “i” existe uma equação diferencial e essas equações não podem ser resolvidas analiticamente para sistemas de muitos corpos. Para possibilitar tal resolução é necessário separá-la em duas partes, uma eletrônica e outra nuclear. Então, multiplica-se a equação 2.16 por 1/c_if_i e a seguinte expressão pode ser observada:

                                  (2.17)

Agora pode se fazer a separação de variáveis entre as partes eletrônica e a nuclear. Vale lembrar que a única consideração que foi feita até agora foi assumir que o potencial é independente do tempo e que nenhuma aproximação foi feita, já que φ_i(r;R) e χ_i(R) são conjuntos completos de funções.

O valor de  é muito pequeno, e sendo dividido por M_a (a massa do núcleo que é cerca de 2000 vezes maior que a massa do elétron) pode-se considerar este valor aproximadamente igual a zero. A mesma consideração pode ser feita para o termo . Essa aproximação é conhecida como aproximação de Born-Oppenheimer. Sendo assim 2.17 pode ser escrita da seguinte forma:

                                       (2.18)

Agora podemos considerar que a localização dos núcleos é constante, como se eles estivessem fixos. Quando isso acontece, tanto o lado esquerdo quanto o lado direito da eq. 2.18 tornam-se iguais a uma constante relativa aos valores fixados para os vetores de distância entre os núcleos. Então, separando-se a parte nuclear da eletrônica teremos duas equações, a primeira expressa a parte nuclear e a segunda a parte eletrônica.

                                                                          (2.19)

                                         (2.20)

            O lado esquerdo das duas igualdades se trata de uma constante de separação. Multiplicando-se os dois termos de 2.20 por –φ_i:

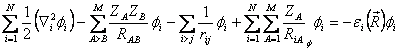                              (2.21)

            O primeiro termo nada mais é que o termo correspondente à energia cinética dos elétrons (T_elf_i), todos os outros termos do primeiro membro são correspondentes à energia potencial (V_elf_i). Sendo assim, a equação de autovalor para a parte eletrônica de uma molécula poliatômica pode ser expressa por:

                                                    (2.22)

Neste caso, a equação para a parte nuclear da molécula pode ser obtida multiplicando-se a eq 2.19 por –χ_i:

            A equação de autovalor para a parte eletrônica de uma molécula poliatômica pode ser expressa por:

                                                               (2.23)

            Onde T_N é o operador de energia cinética referente ao núcleo e  funciona como potencial para o movimento nuclear.

            O Hamiltoniano nuclear é composto pela energia cinética dos núcleos (T_N) e pela energia potencial (ε), neste caso  é responsável por fornecer a expressão de potencial para H_Nucleo. Na verdade o segundo termo é a própria superfície de potencial (SEP) na qual a movimentação nuclear ocorre. Reiterando que o objetivo do trabalho aqui presente é a apresentação de uma metodologia para a obtenção de tal superfície potencial, na verdade uma hiper-superfície potencial, pois, pode assumir a forma de uma função com muitas dimensões (quatro dimensões no caso do H₃⁺).

            Então ε é um autovalor do sistema para cada configuração nuclear, pois depende parametricamente das coordenadas nucleares. Mudando-se as coordenadas nucleares a função que descreve o comportamento eletrônico muda e passa a fornecer um outro autovalor. Tem-se, então, um valor de energia eletrônica para cada configuração nuclear. Achando uma função que forneça os valores das energias eletrônicas em função das coordenadas nucleares fica determinada a função de potencial, e é desejável que se faça isso sem ter que resolver a equação de Schrödinger eletrônica para cada configuração nuclear.

E assim, tendo em mãos a SEP, é possível a resolução da eq. 2.23 e, por conseguinte, a obtenção de valores relativos às propriedades de movimentação de uma molécula como, por exemplo, a resolução de propriedades translacionais, vibracionais e rotacionais, ou no caso de uma reação química, a descrição do processo de colisão entre as moléculas.

2.2 – A SUPERFÍCIE DE ENERGIA POTENCIAL

Agora que já foi definido o que realmente é uma SEP tratar-se-á, a seguir, de algumas de suas propriedades e características desejáveis.

            A SEP é uma função contínua no espaço referente ao sistema em questão. Para se determiná-la de forma real o fator ε deve ser calculado (a partir da eq 2.22) em todas as possíveis configurações nucleares deste espaço configuracional. Tal procedimento é computacionalmente inviável, pois, tomaria muito tempo computacional para ser realizado e seria ainda necessário grande espaço em disco rígido para o armazenamento das variáveis relativas ao processo.

            Um caminho alternativo a este dilema é determinar os valores de ε para uma ampla e representativa gama de configurações geométricas dos núcleos que simulam o processo dinâmico a ser descrito (vibração molecular, colisão atômica, etc...). E então, com base nessas energias determinar uma função analítica (por meio de interpolação e extrapolação) que cubra todo o espaço das coordenas inter-atômicas.

            Na verdade, vale lembrar que se a equação de Schrödinger dependente do tempo pudesse ser resolvida, no caso de sistemas de muitos corpos, não seria necessária a obtenção da SEP.

            Além dos dados dos cálculos ab-initio podem ser usados também dados experimentais na construção da SEP. Por exemplo, informações espectroscópicas podem ser usadas para estabelecer as características dos estados eletrônicos do sistema como, por exemplo, simetria, separação energética entre os estados eletrônicos permitindo assim determinar qual(is) o(s) estado(s) e (são) mais relevante(s) para a composição do sistema. Além disso, com base em informações espectroscópicas dos fragmentos diatômicos do sistema pode-se determinar com precisão as curvas do potencial das moléculas em que se pode determinar o sistema no caso de estudo em que o interesse está voltado para espalhamento.

            Para que uma função analítica possa ser usada como SEP ela deve descrever as interações entre as partículas do sistema e, portanto, ser capaz de reproduzir com a maior precisão possível as informações teóricas (os cálculos ab-initio) e experimentais. Abaixo seguem-se dez critérios usados para determinar se a função analítica pode ser usada como uma SEP [3]:

1. Deve caracterizar com precisão os arranjos assintóticos de qualquer fragmento do sistema completo.

2. Deve ser condizente com as propriedades de simetria do sistema em estudo.

3. Deve descrever o potencial com exatidão e precisão nas regiões de forte interação (a pequenas distâncias) onde se dispõe de informações teóricas e experimentais.

4. Deve representar um comportamento físico razoável nas regiões de interação onde não existem informações.

5. Deve permitir uma transmissão harmônica e suave entre as zonas assintóticas e as de forte interação, sempre buscando um significado físico plausível.

6. A função analítica a ser usada, bem como suas derivadas devem ser as mais simples possível para alcançar a qualidade desejada durante o ajuste bem como para facilitar as operações com a SEP.

7. O número de dados e pontos de cálculo ab-initio deve ser tão pequeno quanto possível para que se possa conseguir um ajuste preciso.

8. Deve convergir à superfície real à medida que mais dados são utilizados.

9. Deve permitir a identificação de quais zonas da superfície são mais críticas e que necessitam de uma maior quantidade de dados para que eles possam ser calculados.

10. Deve possuir a menor quantidade possível de correções ou modificações a serem feitas para que possa ser aplicada a outros sistemas semelhantes.

Os requisitos compreendidos de 1 a 5 são essenciais à SEP e os de 6 a 10 são desejados.

As funções analíticas a serem usadas como base para interpolação e obtenção da SEP mais comuns são empíricas e com parâmetros ajustáveis, contudo, pelo fato de o comportamento do potencial ser de grande complexidade, estas funções devem ser capazes de representar características muito diferentes em zonas distintas da superfície. Isso requer o uso de funções complicadas para que tais comportamentos tão diferentes em parte distintas da superfície possam ser descritos.

Para se obter essa flexibilidade as funções a serem ajustadas apresentam um grande número de parâmetros a serem trabalhados. Contudo, um número muito grande destes causa um problema quanto à otimização dos mesmos podendo conduzir a resultados imprecisos e à não convergência dos parâmetros. Como se não bastassem os problemas que podem surgir, dado o grande número de entidades a serem otimizadas, deve-se levar em consideração o inconveniente proporcionado pelo uso de funções analíticas complicadas.

O uso de funções muito complexas acaba implicando algoritmos nada triviais para a obtenção das derivadas das funções em questão. Isso acarreta o aumento do esforço computacional posterior para se trabalhar com a SEP.

Outra tarefa de extrema relevância para o sucesso de todo esse processo é a escolha adequada de quais pontos ab-initio serão calculados para que se possa fazer o ajuste da função analítica escolhida à SEP. Tal tarefa é, por si só,  objeto de extenso estudo que foge ao escopo deste trabalho, por isso, foi usado um conjunto de pontos que já foi identificado como sendo suficiente para descrever uma SEP e é aceito como referência na literatura [4]. Tal recurso nos possibilitará também uma comparação relativa entre o modelo a ser proposto por este trabalho e o utilizado pelo artigo de referência.

Uma vez determinada a hiper-superfície, o serviço ainda não acabou, é necessário  analisar a sua coerência e isso é feito por meio de uma análise topológica. Uma SEP de três corpos depende de três coordenadas para que se descreva a posição relativa dos átomos do sistema. As outras seis coordenadas que seriam necessárias para estabelecer a posição absoluta dos átomos são as três coordenadas referentes ao centro de massa do sistema tri-atômico e mais três ângulos referentes à orientação do plano formado pelos átomos.

      Como a energia potencial do sistema é uma função exclusiva da sua configuração, ou seja, da posição relativa dos átomos, as seis coordenadas que expressam o centro de massa do sistema e os ângulos de orientação do plano composto pelos três átomos não são variáveis da SEP. A superfície é então uma função de três variáveis e por isso é impossível representá-la em um plano bidimensional. Para contornar esta situação pode se fixar o valor de uma das coordenadas, representando assim a SEP por meio de curvas iso-energéticas em função das outras duas coordenadas.

As formas mais comumente usadas para representar a posição relativa desses três átomos que compõem o sistema são: coordenadas internas nucleares (Figura 2.2) ou duas distâncias nucleares e o ângulo compreendido entre elas (Figura 2.3).

Se o estudo topológico da superfície obtida tem sentido físico, pode-se fazer o uso da SEP para calcular propriedades do sistema e confrontar os resultados obtidos com dados experimentais ou com outros cálculos já consagrados na literatura. No caso de um sistema reativo pode-se usar propriedades como seção de choque ou energia de ativação como padrões de comparação. Já no caso de um sistema molecular podem ser usadas propriedades ro-vibracionais (como espectros).

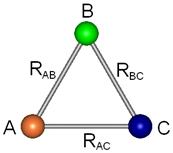
Figura 2.2 – Os três componentes representados na forma de coordenadas internas nucleares.

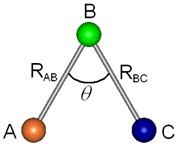
Figura 2.3 – Os três componentes estão representados na forma de duas distâncias inter-atômicas (R_AB e R_BC) e do ângulo q compreendido entre elas (BÂC).

2.3 – MÉTODOS DE AJUSTE E FUNÇÕES ANALÍTICAS A SEREM USADAS.

2.3.1 – Método de ajuste por Splines:

Este método consiste em interpolar-se, localmente, os dados com formas funcionais do tipo polinômios de terceira ordem cujos coeficientes são determinados, assegurando a continuidade da função (e de suas derivadas) entre os pontos ab-initio calculados ou dados experimentais. Este método é direto e flexível, contudo, para eliminar formatos inadequados na SEP é necessária uma grande quantidade de pontos [5].

2.3.2 – Métodos em que potenciais semi-empíricos são ajustados ou corrigidos para reproduzir dados experimentais ou ab-initio:

Os potenciais semi-empíricos são baseados no uso da teoria de orbitais moleculares (que é relativamente simples) para definir uma SEP que, quando ajustada, reproduza os dados experimentais ou mesmo os cálculos ab-initio. Duas são as formas de fazer o ajuste: variar o valor dos parâmetros que surgem de forma natural nos cálculos semi-empíricos, ou então adicionar funções de correção à SEP semi-empírica com o objetivo de ajustar as regiões especiais do potencial (barreiras e poços). Para sistemas triatômicos a forma funcional semi-empírica mais comum é a conhecida como London Eyring Podlanyi Sato (LEPS) [6, 7 e 8]. Entretanto, tal método pode não ser correto o suficiente para que simples ajustes levem a SEP a uma precisão adequada.

2.3.3 – Ajustes empíricos baseados em desenvolvimento de múltiplos corpos:

A idéia fundamental associada a este modelo é a representação da SEP por meio da soma da contribuição das energias potenciais de subpartes do sistema, sendo assim as SEPs de sistemas poliatômicos podem ser simplificadas de forma considerável. Contudo, não é possível controlar o comportamento exibido pela superfície em zonas onde não existem dados disponíveis (pontos ab-initio ou dados experimentais). Este método é conhecido como Many-Body Expansion (MBE) e foi introduzido pelo grupo de Murrel [9]

            No modelo MBE, o potencial proposto, para um sistema de N átomos, é expresso pela seguinte relação:

                                                     (2.24)

            O primeiro termo no lado direito da equação 2.24 representa todos os termos de um corpo apenas, ou seja, de um átomo. Estes termos devem ser nulos quando todos os átomos que compõem a molécula, ou sistema, se dissociam no seu estado eletrônico fundamental. O segundo termo corresponde ao potencial de dois corpos e deve se anular quando a distância entre eles tende a zero. O terceiro representa a interação entre três corpos e seu potencial depende da geometria formada pelos três átomos e deve se aproximar de zero à medida que um dos átomos tende a se afastar dos demais. Finalmente a expressão referente ao ultimo termo representa o potencial de todos os corpos juntos e por isso mesmo depende da posição relativa de todos os átomos.

            No sistema de interesse em questão (envolvendo três corpos) a SEP pode ser escrita da seguinte forma:

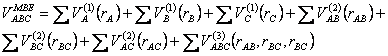                                                                    (2.25)

            Os três termos correspondentes ao potencial diatômico deve ser nulo à medida que a distância entre esses corpos tende ao infinito. Os parâmetros dos termos de dois corpos são determinados de modo a reproduzir as propriedades espectroscópicas dos fragmentos diatômicos do sistema. Já os parâmetros referentes ao potencial dos três corpos (último termo da eq 2.25) são determinados por meio de otimização que devem ser iguais aos valores obtidos pelos cálculos ab-initio menos os valores dos demais potenciais, ou seja:

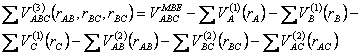                                                   (2.26)

            No caso de um sistema ligado como o H₃⁺ o termo mais relevante é justamente o que representa a interação entre três corpos, ou seja, o termo dado pela equação acima.

2.3.4 – Polinômios em coordenadas físicas:

No modelo MBE original as funções analíticas para descrever o potencial de dois corpos são dadas pelo produto de uma função de amortização e de um polinômio que é função da distância interatômica de interesse. Um tipo de função que descreve as condições acima é a  Rydberg generalizada [10] e pode ser vista logo a seguir:

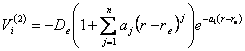                                                                    (2.27)

“D_e” é a energia de dissociação do diátomo, r a distância interatômica e r_e a distância interatômica de equilíbrio. Os valores de a_j podem ser determinados com base em dados espectroscópicos do diátomo ou mesmo por meio de cálculos ab- initio.

            Já a função responsável por representar o potencial do triátomo, e por isso a mais relevante para este trabalho, pode ser expressa como o produto de um polinômio de várias variáveis ρ_i (que nada mais é que o deslocamento das distâncias internucleares em torno da geometria de referência) e de três funções de amortização.  Estas são funções da tangente hiperbólica de ρ_i. Sua expressão pode ser vista logo abaixo [11]:

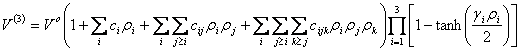                         (2.28)

            Os índices “i”, “k” e “j” representam pares atômicos, o termo “V°” é uma constante, g_i é um fator que determina a velocidade em que o amortecimento leva o valor da função para zero, e ρ_i pode ser expresso pela seguinte expressão:

                                                               (2.29)

r_i representa a distância do diátomo e r_{i, eq} representa a distância de equilíbrio.

            Os coeficientes c_i, c_ij e c_ijk do polinômio são os elementos a serem otimizados para transformar a função 2.28 na SEP de uma molécula triatômica. Esta mesma equação pode ser reescrita da seguinte forma se as coordenadas ρ_i forem substituídas por combinações lineares ortogonais dos ρ_i adaptadas à simetria do sistema:

                                                 (2.30)

            Posteriormente foi proposta uma melhora no modelo MBE proposta por Varandas surgindo então o Double Many Body Expansion (DMBE) [12]. Este método consiste em descrever o potencial do sistema como a soma de um termo proveniente da contribuição do tipo Hartree-Fock e de um termo que representa a correlação eletrônica e desenvolve cada um destes termos segundo a formulação MBE.

            Esses modelos (MBE e o DMBE) apresentam o inconveniente de utilizar polinômios nas variáveis das distâncias internucleares e por isso tendem a divergir quando as distâncias internucleares aumentam, sendo necessário o uso de funções de amortização.

2.3.5 – Polinômios no espaço Bond Order:

Como uma forma alternativa de contornar o impasse citado acima Laganà e Garcia introduziram as coordenadas Bond Order (BO) [13]. A idéia original de usar o BO foi introduzida por Pauling como um parâmetro para a classificação da força da ligação química [14]. A ordem de ligação entre dois átomos A e B pode ser dada por:

                                                                        (2.31)

r_AB representa as distâncias interatômicas, r_eqAB representa a distância de equilíbrio entre esses dois átomos e b_AB é um parâmetro que relaciona a constante de força da ligação. Quando a distância diatômica é igual à de equilíbrio a ordem de ligação é igual a 1. À medida que a distância interatômica cresce o valor da ordem de ligação diminui até que tenda a zero à medida que a separação dos diátomos tende ao infinito. Com uma diminuição do espaço entre “A” e “B” a ordem de ligação aumentará até ser expressa pelo valor exp(b_ABr_eqAB).

            Quando expresso em coordenadas BO o potencial representado por V_i⁽²⁾ pode ser escrito por:

                                                                           (2.32)

i representa os possíveis diátomos presentes no sistema, D_e,i é a energia de dissociação do diátomo e a_ij  são os coeficientes do polinômio. (para a_i1=2 e a_i2=-1 a eq. 2.32 representa o potencial de Morse) [15]. Para polinômios de até quarta ordem (N=4) os coeficientes a_ij podem ser determinados analiticamente por meio de um sistema de equações, fazendo com que esses parâmetros reproduzam as constantes de força espectroscópicas [16]. Já polinômios com graus maiores que este só podem ter seus coeficientes determinados por meio de métodos de otimização.

            O termo de três corpos para um polinômio de grau N e no espaço BO fica representado da seguinte maneira:

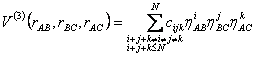                                                                  (2.33)

            Os termos do somatório com i+j+k=i, ou i+j+k=j, ou ainda, i+j+k=k estão excluídos do polinômio pelo fato de se tratarem de termos exclusivamente diatômicos e por isso já são tratados na eq 2.32 e os coeficientes c_ijk são determinados por meio de métodos de otimização.

CAPÍTULO 3

A otimização do potencial por meio do Generalized Simulated Annealing

Otimização nada mais é do que o processo pelo qual determina-se o valor ótimo de uma grandeza em função de um conjunto de parâmetros.  Ou seja, o seu objetivo é achar os valores das variáveis de um processo (ou função) que nos fornecerão o melhor resultado.  Resultado este a ser avaliado por um critério de julgamento preestabelecido. Contudo, uma definição tão simplista não deixa transparecer a real importância dos processos de otimização e nem as dificuldades associadas a eles.

            O maior princípio de otimização já era conhecido há séculos atrás pelos romanos e pode ser expresso pelos seguintes dizeres: “De doubus malis, minus est semper aligendum” (de dois males, escolha o menor).            A otimização é de extrema importância em diversas áreas do conhecimento humano: seja na física, onde pode ser usada para determinar a configuração mais estável ou conveniente de uma molécula; na química, onde procuram-se as condições ideais para a realização de um experimento (quimiometría); na engenharia, onde se deseja relacionar coisas como o fluxo de produção, o gasto de energia; na economia, onde se procura o lucro máximo ou o custo mínimo; na geologia, para estudar-se a prospecção do solo, e, em muitas outras áreas como a estatística, psicologia, biologia e etc...

            Dois tipos básicos de otimização podem ser descritos: a otimização parcial ou local. Na primeira os pontos ótimos locais de funcionamento são o alvo; na segunda   o que interessa é o ponto ótimo absoluto.  Neste trabalho o interesse concentra-se num processo de otimização global.

            A formulação do problema é, talvez, a fase mais importante para otimizar-se um sistema. Tal ação requer, necessariamente, que os elementos essenciais sejam identificados e escritos de forma organizada em uma expressão matemática a partir de definições conceituais (formais ou não).  Quando um problema for traduzido para a sua forma matemática, devemos ter uma função, conhecida como função custo, e as condições de contorno referentes ao problema (essas condições de contorno geralmente se referem a limitações físicas ou econômicas em um sistema).  A função custo geralmente é uma forma de representar o lucro, custo, energia, rendimento, etc., em termos de variáveis de relevância ao processo a elas associado. No caso em questão, a função custo corresponde a um erro representado pela função de desvio quadrático médio e os elementos em questão a serem otimizados serão os coeficientes de um polinômio que descreverá a SEP do sistema em questão (a molécula de H₃⁺).

            Existe um algoritmo genérico de seis passos a serem seguidos para a resolução de um problema de otimização [17]:

· A análise do processo em si, para que se possa explicitar as suas variáveis e as características inerentes ao sistema no qual ele está inserido (colocar o problema em um modelo matemático que o descreva).

· A determinação do critério para a otimização e a especificação da função custo, em termos das variáveis determinadas no primeiro passo (determinar como o modelo matemático, que foi achado no passo anterior, deve ser trabalhado).

• O desenvolvimento, via expressões matemáticas, de um processo válido para a comparação entre as variáveis de entrada e seu respectivo resultado e das variáveis de saída e seu resultado, para validar os resultados (teste de aceitação de resultados).
• Caso a formulação do problema seja muito complicada, deve-se dividir o problema em partes mais manejáveis e/ou simplificar-se a função custo.
• A aplicação de uma técnica de otimização na relação matemática que descreva o problema (escolher uma técnica de otimização e aplicá-la levado em conta os passos anteriores).
• A avaliação da sensibilidade dos resultados às alterações nos coeficientes da função custo e dos parâmetros de entrada no método de otimização.

Os dois primeiros passos foram caracterizados no capítulo anterior e este capítulo irá tratar dos demais.

            Não existe um único algoritmo específico que possa ser aplicado de forma eficiente para a resolução de todos os problemas de otimização. A sua escolha dependerá de cada caso particular e de vários fatores: da natureza dos limites estabelecidos; do número de variáveis dependentes e independentes e das características da função custo e seu comportamento esperado. Os pontos citados de maior importância são os dois últimos, ou seja, o número de variáveis e o comportamento da função custo.  Se a função tivesse apenas um mínimo, qualquer método gradiente seria mais do que suficiente para resolver nosso problema.  Mas, como o comportamento da função custo (uma função de erro que será descrita posteriormente) não é conhecido, o caso mais complicado (o de vários mínimos locais) será associado à função custo em questão.

Para que se possa garantir a localização do mínimo global, o método a ser utilizado não deve ficar preso em mínimos locais e/ou suas vizinhanças (bacias atratoras), e sim, ser capaz de visitar toda a superfície descrita pela função custo, procurando o mínimo global (isto é um problema sério para métodos gradientes).  Independentemente do método de otimização usado, vários ardis estão disponíveis para garantir tal condição, mas todos eles têm suas limitações.

Outro fator a ser observado é o número de variáveis. Por exemplo, um método gradiente seria capaz de achar o mínimo global em uma superfície convexa (um único mínimo), mas o tempo associado a tal tarefa relaciona-se de forma polinomial com o número de dimensões presentes na função custo.  Neste caso, se o número de dimensões for muito grande, uma otimização por métodos gradientes seria inviável por ser computacionalmente muito dispendiosa.  Este é justamente o caso do problema em questão, pois muitas dimensões estão envolvidas.

            Problemas deste tipo, onde um mínimo global deve ser identificado entre vários mínimos, e cuja função custo tem muitas dimensões, são chamados de NP-completos (do inglês Non-Polinomial time complete).  Para este tipo de problema é conveniente a aplicação de métodos de otimização combinatória.

Tais métodos fazem uso de uma função custo, como de costume, mas o espaço sobre o qual a função está definida não é um espaço N dimensional, definido por N variáveis contínuas.  Ao invés disso, o espaço é discreto, embora tenha uma enorme gama de configurações possíveis.

            A otimização por termalização (Simulated Annealing) é uma técnica de otimização combinatória muito conhecida e de ampla aplicação, e foi a base fundamental para a resolução do problema de obtenção da Superfície de Energia Potencial do H₃⁺.

3.1 – SIMULAÇÃO POR TERMALIZAÇÃO OU SIMULATED ANNEALING (SA)

Os métodos de simulação por termalização têm sido aplicados com sucesso na descrição de vários problemas de mínimos globais, além de mostrar-se especialmente eficiente na determinação de mínimos globais localizados entre vários mínimos locais.  Na verdade este método é estocástico e consiste em usar o método de Monte Carlo associado a uma temperatura artificial, que diminui gradativamente à medida que o tempo passa.

            Esta diminuição gradativa de temperatura tenta mimetizar o processo metalúrgico de recozimento (do inglês, annealing), onde um metal derretido é resfriado lentamente para que os átomos do metal em questão tenham a chance de se acomodar na configuração de mínima energia.

Num processo de forja, ou resfriamento muito rápido (do inglês, quenching), os átomos do metal não têm o tempo necessário para se acomodar na configuração correspondente ao mínimo global e acabam ficando presos em uma configuração que descreve um mínimo local.  Portanto, para que se possa garantir que o mínimo global foi atingido é vital controlarmos a redução da “temperatura”.  Na verdade, o nome “temperatura” usado no SA não expressa a temperatura física, é apenas um valor artificial ou um ruído externo que age como uma fonte estocástica que possibilita eventuais escapes de bacias atratoras.  Quando esta “temperatura”  diminuir o suficiente, o SA ficará confinado em uma pequena região em torno do que foi identificado como menor valor.

O desafio inerente a este método está em diminuir a temperatura o mais rápido possível sem que o sistema fique preso em um mínimo local, ou seja, deseja-se determinar um processo de recozimento que seja o mais próximo possível do processo de forja, mas garantindo que o mínimo global seja atingido.

No processo de busca por um mínimo ou no mapeamento de uma hiper-superfície, compara-se o valor resultante da função custo quando dois conjuntos de variáveis, X_t+1 e X_t, são obtidos pela rotina do programa.  X_t seria um vetor N dimensional, que no caso em questão, contém todas as varáveis que tomam parte no processo de otimização.

As configurações para dois passos consecutivos são obtidas da seguinte fórmula:

                                                                    (3.1)

Onde DX_t é uma perturbação randômica nas variáveis relevantes à otimização da função custo e o índice ‘t’ refere-se ao ciclo em que o processo se encontra. A primeira configuração (X_t=0) é um valor inicial qualquer.

O vetor DX_t é fornecido pela rotina do SA da seguinte forma: um vetor aleatório (w) é gerado no intervalo [0,1] com igual probabilidade. Então, aplica-se neste vetor o equivalente ao inverso da integral de uma função de distribuição de visitação (g), ou seja, DX_t = g^‑1(w) e tem-se que:

  (3.2)

Se a função de visitação for baseada na distribuição de Boltzmann-Gibbs, fica definida a máquina de Boltzmann ou Classical Simulated Annealing (CSA) [18, 19 e 20].  Caso a função seja baseada na distribuição de visitação de Cauchy-Lorentz, fica definida a máquina de Cauchy ou Fast Simulated Annealing (FSA) [21]. E por último, caso a estatística usada seja a de Tsallis [22], fica definida a máquina de Tsallis ou General Simulated Annealing (GSA) [23, 24].  Em português, o nome equivalente seria Método Geral de Termalização. Este método é chamado de geral por ser o caso mais geral de estatística a ser usado, o que faz do CSA e do FSA um caso particular do GSA.  

Kirkpatrick et al. [18 e 19] e Ceperley [20], enquanto definiam o algoritmo do CSA, mostraram para sistemas clássicos e quânticos, respectivamente, que a probabilidade de se obter o mínimo absoluto do sistema usando o SA é igual a 1.  Também foi provado que, para o caso clássico, a única condição necessária para ter- se a probabilidade de obtenção do mínimo global igual a 1 seria uma diminuição logarítmica da temperatura com o tempo.  Szu e Hartley [21] provaram que o resfriamento podia ocorrer de forma muito mais rápida e eficiente se a temperatura diminuísse com o inverso do tempo.

3.2 – O GENERAL SIMULATED ANNEALING (GSA)

O ponto central do GSA está na estatística de Tsallis que, baseado na teoria de multifractais, propôs uma generalização da entropia.  A entropia de Tsallis tem a seguinte fórmula:

                                                                  (3.3)

            Onde q Î R, p_i são as probabilidades das configurações microscópicas e k é uma constante positiva.  No limite de ‘q’ tendendo a um, a equação de entropia de Tsallis fica reduzia à fórmula usual da entropia de Boltzmann-Gibbs, ou seja:

                                                           (3.4)

            Otimizando-se (3.2) no ensemble canônico teremos:

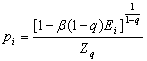                                                         (3.5)

onde

                                                   (3.6)

            A variável representada por b é um multiplicador de Lagrange e vale 1/kT e E_i é o espectro da energia do sistema em questão. Mais uma vez, se q for substituído por um em (3.5) e (3.6) teremos as equações referentes à estatística de Boltzmann-Gibbs.  Ou seja, se q=1, a função de visitação (g_qv) presente em (3.2) é baseada em (3.5) e (3.6) e teremos o CSA.  Já se q=2, então, g_qv presente em (3.2) nos fornecerá o FSA.

            Obtendo-se a função de visitação para a estatística de Tsallis [25] temos o seguinte:

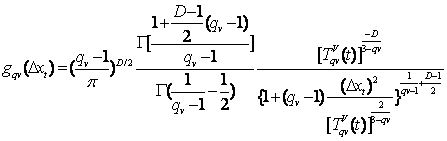                                         (3.7)

Onde, D refere-se ao número de dimensões a participarem da otimização, q_v é um parâmetro a ser acertado, T_qv^V é a temperatura do sistema no instante do cálculo de DX_t e G é a representação de uma função gama. Em 3.7, se o valor de q for igual a um teremos o CSA, se q for igual a dois a função 3.7 passará a refletir o modelo do FSA e no caso de o valor de q ser igual ou maior que três a distribuição passa a ser não normalizável como mostrado em [26]. Para que se possa ilustrar como o valor de q_v afeta o calculo de ΔX basta que se observem as duas figuras a baixo. Elas mostram a progressão de saltos dados pelo GSA para uma dimensão ao longo do tempo. A única diferença entre elas é que o q_v de uma é de 1, 5 (Figura 3.1) e o da outra é de 2,5 (Figura 3.2).

Contudo, antes de calcular-se o DX_t é necessário definir a temperatura referente àquele instante.  Para o cálculo da temperatura usa-se a seguinte expressão:

                                                                               (3.8)

            Vale lembrar que: t não é o tempo real e sim o ciclo na qual o cálculo se encontra; T_q(1) nada mais é do que a temperatura inicial do sistema e que o parâmetro q pode ser o mesmo a ser usado em (3.7), ou seja, q_v ou então pode assumir um valor diferente que recebe o nome de q_T.  Na máquina de Boltzmann tanto q_v como q_T são 1 o que faz com que a expressão de temperatura fique da seguinte forma:

                                                                                                      (3.9)

Figura 3.1 – Saltos gerados pelo GSA na dimensão X quando o q_v usado é de 1,5.

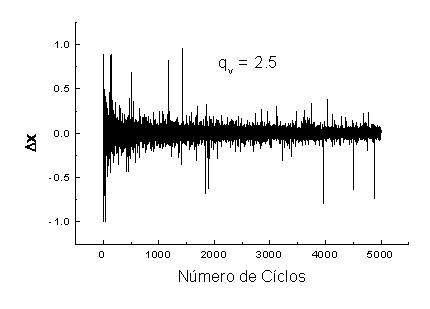
Figura 3.2 – Saltos gerados pelo GSA na dimensão X quando o q_v usado é de 2,5.

            Analisando as duas figuras acima, fica claro que quanto maior o valor de q_v mais rápida será a redução do tamanho dos ΔX gerados ao longo do tempo.

            Já na máquina de Cauchy a temperatura é determinada pela expressão abaixo:

                                                                (3.10)

Todo o processo do GSA só terá sido completamente descrito quando a probabilidade de aceitação (P_qa) for definida.  Para tal vamos usar um exemplo: o de relação entre configuração espacial (x) e energia (E(x)).   Calcula-se a energia para um instante t representada por E(x_t) e depois para um instante t+1 representada por E(x_t+1). Se E(x_t+1) < E(x_t) então o valor está mais próximo de um mínimo portanto, será aceito.  Contudo, se E(x_t+1) > E(x_t) o valor pode ser aceito ou não, dependendo da P_qa e de um número gerado aleatoriamente. Se esse valor randômico for menor do que P_qa a configuração gerada é aceita, mesmo havendo um aumento na energia.  O valor de P_qa pode ser calculado pela seguinte fórmula:

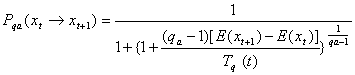                             (3.11)

            Dito tudo isso, devem-se voltar as atenções para a solução de como calcular o valor de DX_t, que foi expresso na equação 3.2, como sendo o inverso de uma função de distribuição.

No caso de distribuição generalizada a equação com a qual deve se trabalhar é 3.7. Por isso mesmo temos que integrá-la num intervalo indo de zero a “x” para que se possa obter um número aleatório que estará associado à probabilidade de ocorrência. Tal número randômico (rand) pode ser descrito pela seguinte fórmula.

                                (3.12)

            A parte da eq. 3.12 referente à integral pode ser abreviada da seguinte forma:

                                                                                       (3.13)

            Esta integral só tem solução analítica quando “c” é igual a dois. Em casos mais gerais a sua solução pode ser obtida por meio da série expressa logo abaixo.

          (3.14)

            A eq. 3.14 pode ser expressa de forma genérica dando a seguinte expressão:

                                                          (3.15)

            A expressão acima, para efeitos computacionais, é considerada até os termos de décima sexta ordem. Tal procedimento é baseado no fato dos valores das ordens superiores serem, praticamente, irrelevantes para o valor do salto expresso por Dx_t.

            Mas, como está expresso na eq. 3.2, o que nos interessa não é a integral em si e sim o seu inverso, sendo assim, o que vem a ser relevante não é 3.15, mas, o seu inverso.

O problema de inverter funções [26] que se encontram na forma de uma série de potência é razoavelmente comum. Então, se a série em questão apresenta a forma geral mostrada abaixo:

                                                              (3.16)

            Sua forma inversa é:

                                                                         (3.17)

            A fórmula expressa imediatamente acima, ou seja, a 3.17 tem sua autenticidade baseada num teorema que diz: “Sendo f(z) uma função analítica em z=a, e f´(a)¹0, então a inversa de f(z) existe e é analítica em uma região suficientemente pequena no entorno de f(a) e sua derivada é 1/f´(a).”

            Os coeficientes b_n, que estão presentes em 3.17 podem ser deduzidos empregando-se a fórmula de Cauchy. Usando f(z) como variável independente, a integral que inclui em seu contorno o pólo z=w, pode ser posta na forma:

                                                                                 (3.18)

            Uma vez que 3.18 é diferenciada em “w” e integrada por partes ela se torna:

                                                                                     (3.19)

            Expandindo-se o denominador presente na eq 3.19 (processo abaixo),

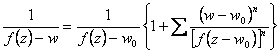                                                           (3.20)

Substituindo-se 3.20 em 3.19 e comparando-se com a equação referência (eq. 3.17) diferenciada em “w”, pode-se determinar b_n, ou seja,

                                                                              (3.21)

            Resolvendo-se a integral de 3.21 ter-se-á:

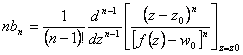                                                                     (3.22)

ou seja,

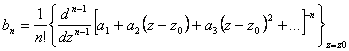                                                      (3.23)

ou ainda:

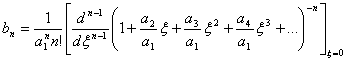                                                      (3.24)

            A equação de recorrência para os coeficientes b_n pode ser resolvida por uso do teorema multinomial:

onde

            Introduzindo-se a expansão multinomial tem-se:

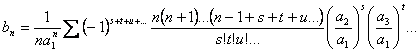                                     (3.25)

onde

            Então, com base na eq 3.25 os cinco primeiros termos da série invertida são:

                                                                                 (3.26)

                                                                             (3.27)

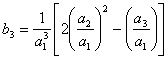                                                                (3.28)

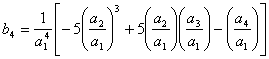                                                              (3.29)

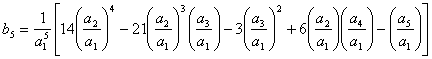                                 (3.30)

            Como o polinômio da expressão 3.15 só tem os termos ímpares, em sua inversa os termos pares serão nulos, deste modo, os primeiros coeficientes do inverso da série de potência 3.15 serão:

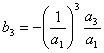
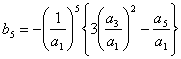
            Todavia, embora os coeficientes sejam os valores exatos da série, não pode ser esquecido que esta é, na verdade, uma aproximação de Dx_t. Então, o inverso da série pode ser expresso da seguinte forma:

                             (3.31)

            Substituindo-se os valores de 3.12 em 3.15, o valor da perturbação Dx_t passa a ser expresso pela fórmula:

                                  (3.32)

            Escolhe-se um número aleatório (rand) num intervalo fechado de zero a um e substitui-se esse valor em 3.31 e a expressão imediatamente acima nos fornece o incremento Dx_t. A partir daí, por indução, as coordenadas de um vetor de “D” dimensões serão demonstradas como proposto inicialmente por Tsallis et al [24].

Para uma dimensão (D=1)

Para duas dimensões (D=2)

Para três dimensões (D=3)

Para mais de Três dimensões (D>3)

                                           (3.33)

...

                                 (3.34)

(a resolução numérica acima pode ser vista em mais detalhes em 25)

            Como já havia sido dito, a parametrização das equações é feita levando-se em conta, q_a, q_v, q_t e, além disso “D” (o número de dimensões).  Vale a pena ressaltar que por causa do processo de recozimento (annealing) a função de distribuição de visitação “estreita-se” ao longo do processo causando uma diminuição nos saltos provocados pelo Dx_t.

            Sabe-se que são gerados D - 1 números aleatórios (os números “rand”) a cada passo do processo. No caso da primeira componente x_t+1⁽¹⁾ (eq. 3.33), ela é composta por apenas um número randômico no intervalo [0,1] (rand⁽¹⁾), já a componente x_t+1⁽²⁾ é composta por dois números aleatórios (também no intervalo compreendido entre [0,1]) e assim segue até x_t+1^(D-1) e x_t+1^(D) que têm em sua expressão todos os D–1 números rand que foram gerados. Desta forma, as primeiras coordenadas são privilegiadas com relação às ultimas, e isso nos permite chegar à conclusão de que as equações não são capazes de fornecer a simetria necessária para o método, causando uma “deformação” das últimas coordenadas fazendo com que a “visitação” da SEP seja mais eficiente em algumas dimensões do que em outras.

3.3 – AJUSTES PROPOSTOS E ALGORITMO UTILIZADO

Para transpor essa dificuldade, o algoritmo da GSA passou a ser planejado para que todas as D componentes do problema fossem tratadas como vetores unidimensionais e independentes.

            Ademais, outros problemas passaram a ser percebidos, como por exemplo, o uso do inverso da função g (eq. 3.2), causa alguns inconvenientes, dentre eles tem-se: o resultado do salto em uma das dimensões pode variar enormemente indo de zero e até mesmo resultados tendendo ao infinito ou os cálculos podem se tornar muito complicados e computacionalmente dispendiosos.

            Para resolver tais problemas optou-se por adotar a função g(w) diretamente e não mais o inverso dela como fonte geradora do vetor Dx_t. Fazendo-se isso o tempo computacional foi consideravelmente reduzido.  A função passa a gerar valores entre zero e um, permitindo multiplicá-los por um número conveniente, possibilitando-se modular a extensão dos saltos, mantendo-os dentro de limites adequados, sem prejudicar os resultados. Matematicamente tal fenômeno pode ser explicado pelo fato de a função g(w) poder muito bem ser o inverso normalizado de uma outra função de distribuição de visitação que também obedeça à estatística do modelo adotado (Boltzmann, Cauchy-Lorentz ou Tsallis).

            Uma vez que todo o método para a otimização foi definido, fica claro o algoritmo a ser seguido para que se possa usar o GSA em um processo de otimização.  Definir-se-á uma função custo geral L(x) e a partir dela será descrito o algoritmo:

I. Tem-se, então, um conjunto de cinco parâmetros de entrada a serem definidos, q_a, q_v, q_T, T(1) (temperatura inicial) e x₁ (configuração inicial) (t inicial é sempre 1).  Se q_a, q_v e q_T forem (1,1,1) teremos o CSA e se forem (1,2,2) teremos o FSA.

II. Usa-se g_v para gerar, aleatoriamente, uma configuração x_t+1 a partir da configuração anterior (x_t).

III. Calcula-se o valor de L(x_t+1) e se compara com o valor de L(x_t):

i. Se L(x_t+1) < L(x_t),  armazena-se o valor de x_t+1 no lugar de x_t.

ii. Se L(x_t+1) > L(x_t),  gera-se um número aleatório r Î [0,1] e calcula-se P_qa de acordo com (3.11).

a. Se r < P_qa. conserva-se o valor de x_t.

b. Se r > P_qa ,substitui se o valor de x_t por x_t+1.

IV. Calcula-se a nova temperatura usando-se (3.8).

V.

Sim

Sim

Repete-se o procedimento de II a IV até que o critério de convergência tenha sido alcançado ou que o número máximo de loops seja esgotado.

Tendo o método já esclarecido de forma genérica, ele agora pode ser aplicado ao problema específico proposto neste trabalho.

Segue um fluxograma explicativo do algoritmo apresentado.

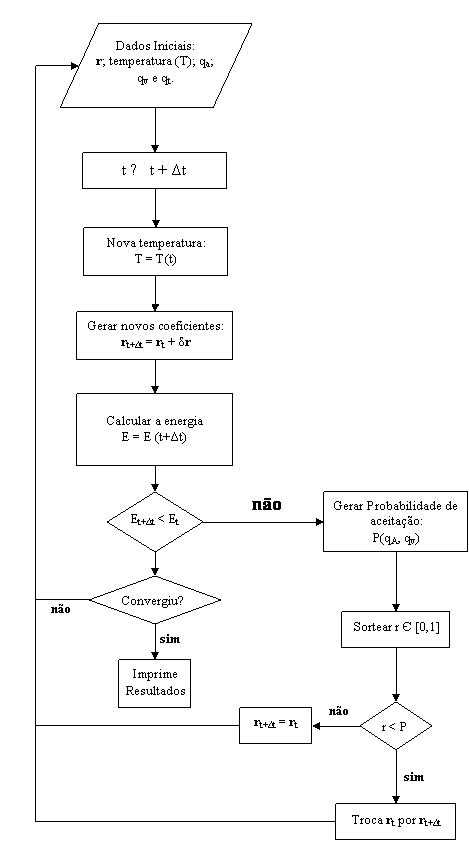
Figura 3.3  – Fluxograma representativo do algoritmo do GSA.

CAPÍTULO 4

Determinando a SEP: otimização do potencial por meio do GSA

4.1 – APLICAÇÃO DO GSA NO CASO ESPECÍFICO DE AJUSTE DE SEP´s

            Levando-se em consideração os seis passos usados para resolver um problema de otimização, a primeira coisa seria definir as variáveis cujos valores ótimos quer-se descobrir.  Na verdade é desejado se fazer um ajuste da SEP usando-se a seguinte função:

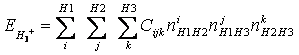                                            (4.1)

Onde C_ijk corresponde aos valores dos coeficientes de cada membro do polinômio representado por (4.2) e m é dado pela seguinte expressão:

                                                            (4.2)

R_eqH1H2 é a distância de equilíbrio entre os átomos H1 e H2 (0,873354Å) e R_H1H2 é o valor da distância entre eles.  Já b é uma constante espectroscópica que só tem sentido quando se fala em sistemas diatômicos.  Partindo destes princípios, as variáveis a determinar seriam os coeficientes C_ijk e os valores de b.  Posteriormente percebeu-se que não seria necessária a otimização envolvendo b já que cada h é na verdade uma relação diatômica e sendo assim o valor assumido para b foi de 1,9420Å^-1.

            Feito isso, deve-se determinar a função custo. Esta função é uma função de erro conhecida como c² e ilustrada pela equação abaixo:

                                            (4.3)

            Onde E_exp é o valor das energias calculadas por métodos ab initio, ou seja, os pontos de partida para a construção da SEP.  E_cal é o valor calculado das energias para as mesmas geometrias usadas em E_exp, só que para este cálculo usou-se o polinômio expresso em (eq. 4.1) com os valores dos coeficientes obtidos pelo método de otimização.  Então, gera-se pelo método GSA (a escolha do método de otimização) um conjunto de coeficientes e calcula-se a função erro, gera-se novamente um outro conjunto de coeficientes (de acordo com a secção 2.1) e também calcula-se o erro, caso o erro tenha diminuído, aceita-se o conjunto de coeficientes.  Caso tenha aumentado existe uma chance de ser aceito, dependendo do procedimento explanado na secção 2.2 e a eq. 2.11 (processo para a comparação entre as variáveis de entrada e saída e seus respectivos resultados).

             Os passos quatro e seis do algoritmo genérico para uma otimização, apresentados no capítulo 3, não foram necessários.

            Ao contrário do uso comum do GSA para se fazer um estudo da SEP como método de otimização global da geometria usa-se este processo para a determinação do mínimo absoluto da função de erro, variando-se randomicamente os coeficientes da eq. 4.1.

            Como foi dito, de início o b também era uma variável a ser otimizada, contudo o processo não convergia.  Variou-se o valor inicial dos parâmetros de entrada do GSA (q_v, q_T, q_a e T(1)), mas mesmo assim a convergência não foi alcançada. Percebeu-se então que, ao mudar o valor de b, a família do polinômio também estaria sendo mudada automaticamente.  Assim, para cada família teríamos um conjunto ótimo de coeficientes.  Resolveu-se este problema mantendo um valor fixo para b e variando apenas os coeficientes C_ijk, ou seja, pode-se transformar um processo de otimização não-linear em um linear.

            Outro problema enfrentado foi o da simetria inerente à molécula H₃⁺.  Dois meios foram propostos para que tal impasse fosse evitado: um deles seria aplicar a simetria por sobre as configurações usadas para os cálculos (o que praticamente triplicaria o número de pontos); e o outro seria achar quais combinações de i, j e k nos dariam os mesmos valores (o que diminuiria o número de variáveis a serem otimizadas).  O primeiro caso tornaria os cálculos mais demorados e o segundo os aceleraria, optou-se então pelo segundo caso.

            Pelo fato de a molécula ser homonuclear,  qualquer combinação dos valores de i, j e k fornecerá o mesmo resultado, ou seja, se tivermos o conjunto (1,0,0) ou o conjunto (0,1,0) ou mesmo (0,0,1) teremos o mesmo resultado de C_ijk hⁱ h^j h^k, afinal, h¹ h⁰ h⁰ será igual a h⁰ h¹ h⁰ que por sua vez será igual a h⁰ h⁰ h¹ e portanto seus coeficientes devem ser iguais.  Por isso é mais prático definir apenas C₁₀₀ e repetir seu valor ótimo para C₀₁₀ e para C₀₀₁. Os coeficientes de 1 a 12 servem pra descrever única e exclusivamente o estado espalhado e, como o objetivo deste estudo é o estado ligado, eles podem simplesmente ser mantidos com o valor igual a zero.

            Para tornar mais claro o processo, o algoritmo do GSA em sua forma específica para este caso em questão pode ser visualizado a figura 4.1.

Figura 4.1- Fluxograma representativo do algoritmo do GSA para este sistema.

4.2 – RESULTADOS OBTIDOS

Como foi visto, no começo havia setenta e oito parâmetros a serem otimizados, eliminando-se b e os doze primeiros coeficientes e, fazendo aplicação das propriedades de simetria, obteve-se apenas dezesseis parâmetros a serem otimizados o que tornou o processo de convergência tão rápido que foi desnecessário (e até impossível) um estudo de sensibilidade do método aos parâmetros de entrada (q_v, q_T, q_a, T(1) ), visto que a convergência era praticamente imediata.

            A lista de coeficientes equivalentes é a seguinte:

Tabela 4.1 – Lista de índices e coeficientes que compõem a SEP.

Número do conjunto	Números dos coeficientes	Índices de i, j e k	Valor dos Coeficientes
1	13, 28, 33	0,  1,  1	-151.2698248336
2	14, 18, 29, 38, 48, 52	0,  1,  2	-23.1254123308
3	15, 22, 30, 42, 62, 65	0,  1,  3	-19.9060287748
4	16, 25, 31, 45, 71, 73	0,  1,  4	32.8491412104
5	17, 27, 32, 47, 76, 77	0,  1,  5	20.2972242420
6	19, 49, 56	0,  2,  2	166.7052878958
7	20, 23, 50, 59, 63, 68	0,  2,  3	-16.7463435443
8	21, 26, 51, 61, 72, 75	0,  2,  4	-61.6939891829
9	24, 64, 70	0,  3,  3	60.5723800865
10	34	1,  1,  1	248.7354190812
11	35, 39, 53	1,  1,  2	29.6831532325
12	36, 43, 66	1,  1,  3	-81.2493879566
13	37, 46, 74	1,  1,  4	-7.2215508355
14	40, 54, 57	1,  2,  2	-90.1410739836
15	41, 44, 55, 60, 67, 69	1,  2,  3	39.0215482771
16	58	2,  2,  2	-14.7916875379

Com esses coeficientes a equação 3.1 pode ser determinada de tal forma que expressa o objeto de estudo em questão: a SEP da molécula de H₃⁺. Com essa função em mãos, as energias de cada um dos pontos ab initio utilizados pode ser calculada e comparada com a energia dada como real. Na tabela abaixo encontram-se os valores das distâncias usadas (R₁, R₂ e R₃) em angstron, suas energias calculadas via ab initio [27], a energia calculada usando a SEP com os coeficientes acima (E_cal) e o erro entre eles (todas essas energias em kcal/mol).

Tabela 4.2 – Relação de configurações e energias (início):

R1	R2	R3	Energia(ab initio)	Energia(GSA)	Erro
0,6234	0,6234	0,6234	-787,71330	-787,36259	-0,3507
0,6777	0,6777	0,6777	-813,37846	-813,28841	-0,0901
0,7367	0,7367	0,7367	-830,38398	-830,43514	0,0512
0,8015	0,8015	0,8015	-839,92214	-840,03865	0,1165
0,8731	0,8731	0,8731	-842,93418	-843,05519	0,1210
0,9534	0,9534	0,9534	-840,17314	-840,20259	0,0295
1,0445	1,0445	1,0445	-832,14101	-832,01036	-0,1306
1,1499	1,1499	1,1499	-819,15155	-818,88263	-0,2689
1,2751	1,2751	1,2751	-801,45577	-801,18099	-0,2748
1,4290	1,4290	1,4290	-778,80266	-779,34079	0,5381
0,5422	1,1306	1,1306	-777,79864	-777,65971	-0,1389
0,6109	1,0564	1,0564	-807,47987	-807,10889	-0,3710
0,6875	0,9896	0,9896	-827,56019	-827,42438	-0,1358
0,7739	0,9289	0,9289	-839,16912	-839,21653	0,0474
0,8217	0,8217	0,9896	-839,16912	-839,26817	0,0990
0,7739	0,7739	1,1306	-827,74844	-827,77919	0,0307
0,7293	0,7293	1,3093	-808,17013	-807,97313	-0,1970
0,5535	0,6613	0,6613	-780,81069	-780,82734	0,0166
0,5875	0,5875	0,7015	-781,12445	-781,14968	0,0252
0,5343	0,7628	0,7628	-788,96832	-789,35921	0,3909
0,6022	0,7189	0,7189	-807,47987	-807,46400	-0,0159
0,6389	0,6389	0,7628	-807,73087	-807,71536	-0,0155
0,6022	0,6022	0,8603	-790,91360	-791,34222	0,4286
0,5156	0,8824	0,8824	-781,75196	-781,85221	0,1003
0,5816	0,8302	0,8302	-809,55065	-809,40776	-0,1429
0,6547	0,7819	0,7819	-825,30115	-825,30431	0,0032
0,6945	0,6945	0,8302	-825,48940	-825,48692	-0,0025
0,6547	0,6547	0,9389	-810,80567	-810,83387	0,0282
0,6171	0,6171	1,0686	-786,33278	-786,47308	0,1403
0,5616	0,9638	0,9638	-798,44372	-797,98008	-0,4636

Tabela 4.2 – Relação de configurações e energias (continuação):

R1	R2	R3	Energia(ab initio)	Energia(GSA)	Erro
0,6324	0,9052	0,9052	-822,03810	-821,79501	-0,2431
0,7117	0,8514	0,8514	-835,52956	-835,57399	0,0444
0,7551	0,7551	0,9052	-835,65507	-835,69006	0,0350
0,7117	0,7117	1,0279	-822,79111	-822,67931	-0,1118
0,6709	0,6709	1,1782	-800,95376	-800,71644	-0,2373
0,5900	1,2519	1,2519	-784,70125	-784,99821	0,2970
0,6641	1,1639	1,1639	-809,73890	-809,79220	0,0533
0,7474	1,0862	1,0862	-826,86993	-826,94484	0,0749
0,8425	1,0165	1,0165	-836,84734	-836,93324	0,0859
0,8957	0,8957	1,0862	-836,84734	-836,92208	0,0747
0,8425	0,8425	1,2519	-826,61892	-826,77530	0,1564
0,7933	0,7933	1,4724	-808,67214	-808,74622	0,0741
0,6416	1,4000	1,4000	-784,88951	-785,45856	0,5690
0,7219	1,2920	1,2920	-806,03659	-806,33189	0,2953
0,8133	1,1990	1,1990	-820,65758	-820,79199	0,1344
0,9190	1,1173	1,1173	-829,25446	-829,23124	-0,0232
0,9788	0,9788	1,1990	-829,19171	-829,15769	-0,0340
0,9190	0,9190	1,4000	-819,84181	-820,08578	0,2440
0,8640	0,8640	1,6881	-803,02455	-803,21337	0,1888
0,6974	1,5902	1,5902	-778,92816	-778,76273	-0,1654
0,7852	1,4503	1,4503	-796,68670	-796,79389	0,1072
0,8862	1,3346	1,3346	-809,17415	-809,23384	0,0597
1,0052	1,2360	1,2360	-816,64151	-816,48263	-0,1589
1,0737	1,0737	1,3346	-816,51601	-816,34404	-0,1720
1,0052	1,0052	1,5902	-807,85637	-807,93473	0,0784
0,8550	1,6579	1,6579	-781,87746	-780,98392	-0,8935
0,9681	1,5048	1,5048	-792,67063	-792,41768	-0,2530
1,1042	1,3802	1,3802	-799,19674	-798,99960	-0,1971
1,1842	1,1842	1,5048	-799,00848	-798,78531	-0,2232
1,1042	1,1042	1,8567	-790,66260	-790,34478	-0,3178
1,220	1,5641	1,5641	-776,73188	-777,13294	0,4011
1,3166	1,3166	1,7333	-776,48087	-776,80900	0,3281
0,6004	0,7367	0,9080	-810,17816	-810,12249	-0,0557
0,7096	0,8731	1,0898	-827,62294	-827,60474	-0,0182
0,8400	1,0445	1,3400	-820,21832	-820,44541	0,2271
0,5414	0,7367	1,0134	-784,07375	-784,18230	0,1086

Tabela 4.2 – Relação de configurações e energias (final):

R1	R2	R3	Energia(ab initio)	Energia(GSA)	Erro
0,6406	0,8731	1,2317	-807,79362	-807,57696	-0,2167
0,7572	1,0445	1,5571	-804,53057	-804,86047	0,3299
0,5781	0,8731	1,4118	-778,55166	-778,33683	-0,2148

Dados de calculo ab initio  de [28]

            Agora, de posse da SEP, certos testes devem ser feitos para verificar se ela expressa, ou não, uma realidade física aceitável. O primeiro passo seria uma análise gráfica da SEP, procurando regiões espúrias ou comportamentos inaceitáveis. Outro ponto a ser observado é se as propriedades calculadas com base na SEP obtidas têm significado real e relevância se, se forem comparadas a outras SEP´s da literatura.

4.3 – INTERPRETAÇÃO DOS RESULTADOS OBTIDOS

A primeira forma básica de comprovar os resultados obtidos é observar o erro associado às energias ab-initio e as obtidas pela SEP, e observando a tabela 4.2 fica claro que a diferença máxima de energia existente foi de 0,8935 kcal/mol (um erro da ordem de 0,1%) e a mínima foi de 0,0025 Kcal/mol, e tais erros estão abaixo do aceitável para uma SEP.

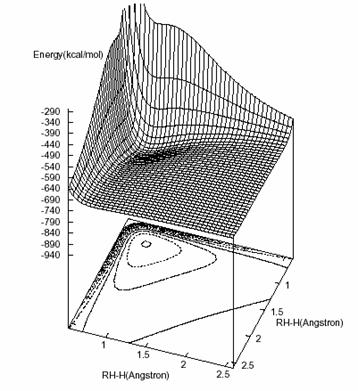
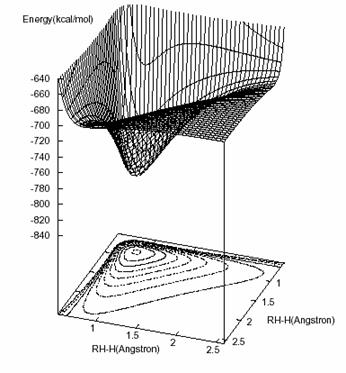
Figura 4.2 – Duas representações gráficas da SEP em ângulos diferentes

O passo seguinte é analisar o aspecto gráfico da SEP, só que ela não pode ser representada com todas as suas variáveis. Então o que se faz é escrever a função de forma dependente de R₁ e R₂ e o ângulo q entre essas distâncias (a passagem de R₃ para q e vice-versa pode ser feita pela lei dos co-senos, ver figura 2.3).  Fixando-se q pode-se, então, construir um gráfico da energia (obtida por meio do polinômio que foi determinado) em função das duas distâncias.  Se q for fixado em 60^o (o ângulo que deve compreender a energia mínima) teremos a figura abaixo da SEP.

No plano inferior da figura podemos ver o contorno das energias contido no intervalo de –841,8 e –141,8 Kcal/mol, e essas curvas são espaçadas umas das outras de 35 em 35 Kcal/mol e, como pode ser observado, o formato da SEP obtida é similar ao da melhor SEP presente na literatura [28].

 Para que possa obter-se uma comparação mais efetiva entre a SEP aqui proposta e aquela que é considerada como referência mais atual na literatura e dados experimentais foram calculados os níveis vibracionais do H₃⁺ para o momento rotacional igual a zero (j=0). Estes cálculos foram feitos usando como base o Método do Elemento Finito (MEF), e usando coordenadas hiperesféricas [29] para ambas as SEP´s.

      Mas é relevante citar que a obtenção dos níveis de energia depende do método usado e, por isso as energias vibracionais da SEP de Jaquet, além de obtidos diretamente também foram melhoradas usando o programa TRIATOM de Tennyson e Miller [30], que usa um conjunto de bases finito de representação. Seguem, na tabela 4.3 os resultados para que possam ser comparados:

Tabela 4.3 – Energias vibracionais experimentais e de SEP´s diversas.

Nível	GSA (cm^-1)	Jaquet (cm^-1)	Tennyson (cm^-1)	Experimental (cm^-1)
1	2521,3	2521,20	2521,465	2521,409
2	3178,4	3178,15	3178,315	3178,290
3	4777,0	4778,01	4778,370	4778,350
4	4997,3	4997,73	4998,055	4998,045
5	5553,7	5553,95	5554,155	5554,155

CAPÍTULO 5

Conclusões

Com base no objetivo primário deste trabalho (ou seja, determinar uma metodologia para a obtenção da hiper-superfície de Energia da molécula de H₃⁺) é possível afirmar-se que ele foi cumprido já que a SEP obtida apresenta resultados satisfatórios. Como pode ser visto, tanto por sua forma (figura 4.1) como pelas energias calculadas usando-se a superfície (tabela 4.2), os resultados são mais que satisfatórios.

Tomando-se por base a tabela 4.3, pode ser observado que o maior erro entre os valores obtidos usando-se a SEP pela metodologia proposta e os valores medidos experimentalmente são da ordem de 0,03%, validando assim a SEP obtida ao longo deste processo. Ela também pode ser comparada com os resultados obtidos da referência na literatura.

Contudo, também ficou claro que a metodologia proposta pode ser estendida a outros sistemas moleculares triatômicos por se tratar de uma metodologia rápida e eficiente. Para que se possa fazer tais afirmações, tomaram-se por base os pontos da sessão 2.2, nos quais são citados os critérios para determinação da eficiência e/ou aceitabilidade de uma função como uma SEP. O método proposto se enquadra facilmente nos pontos presentes naqueles dez itens.

A ênfase do processo deve ser mantida em dois pontos principais: a função analítica que foi usada para tecer a SEP e o uso do Generalized Simulated Annealing como método de otimização. O foco deve ficar nesses dois pontos principais porque, até por questões de normalização para posteriores comparações, os outros pontos críticos para a obtenção de uma hiper-superfície foram buscados da literatura para que os resultados pudessem ser confrontados.

Os outros pontos críticos são a definição no nível de calculo ab-initio a ser utilizado, as correções necessárias e suficientes e quais pontos no espaço devem ser escolhidos para que a partir da função analítica proposta possa se chegar à SEP. Como foi dito estes pontos foram os mesmos do trabalho usado como referência para que os resultados pudessem ser confrontados de forma direta (tabela 4.3) para que os resultados da metodologia proposta ficassem claros e fossem os mais conclusivos  possíveis, como realmente o foram.

Como perspectivas, este trabalho pode ser estendido a aglomerados de H_n⁺ ou mesmo a outros sistemas poliatômicos com mais de três átomos, afinal, o funcionamento geral do método pode ser estendido para muitas outras dimensões.

Outro ponto que poderia ser investigado no futuro seria a eficiência do método com relação aos parâmetros de entrada, ou seja, um estudo para se otimizar os valores de q_v, q_a, e q_t, ou mesmo propor um método que tenha uma rotina de alta otimização varrendo alguns destes valores ao longo do processo para que uma convergência mais rápida possa ser atingida. Para este sistema, em particular, isto não foi um problema devido à rápida convergência, contudo, para sistemas mais complexos, tal aspecto pode ser vital para que a viabilidade computacional do método possa ser mantida.

E, por ultimo, talvez um estudo para aplicações de outras funções custo para o método, não só χ² (equação 4.3). Pode-se, também, tentar otimizar a própria função analítica responsável pela SEP (equação 4.1) para que se possa reduzir o número de coeficientes. Neste caso a única otimização feita neste aspecto foi a aplicação da geometria para evitar a redundância dos coeficientes, acelerando-se assim a convergência do processo. Na verdade, em um primeiro instante a simetria foi ignorada e os coeficientes redundantes obtidos tendiam a convergir para um mesmo valor, chamando assim a atenção para o fato de a molécula apresentar uma simetria era algo a ser levado em consideração.

É importante ressaltar que a introdução desta nova metodologia colocou o nosso grupo de pesquisa entre os poucos grupos internacionais que conseguem produzir superfícies de potencial próprias para o estudo da dinâmica de reação de núcleos.

Bibliografia

1. Levine, Ira N., Quantum chemistry. 4ed. Englewood Cliffs, New Jersey, USA: Prentice Hall, 1991. p 1-19.
2. Szabo, Attila; Ostlund, Neil. Modern quantum chemistry: introduction to advanced electronic structure theory. 1ed. New York, New York, USA. McGraw-Hill, 1989. p 40-97.
3. Gargano, Ricardo. Superfície de energia potencial: conexão entre a estrutura eletrônica e a dinâmica molecular. In: Escola Brasileira de Estrutura Eletrônica, 2002, Juiz de Fora. Escola de estrutura eletrônica. São Paulo, SP. Livraria da Física, 2003. p 43-5.
4. W.Cencek, J. Rychlewski, W. Kutzelnigg, J. Chem. Phys., 108 (1998) 2831.
5. Laughline, D. R. and Thompson,  D. L., J. Chem. Phys., 59 (1973) 4393.
6. London, F., Z. Electrochem, 35 (1929) 552.
7. Sato, S., J. Chem. Phys., 23 (1955) 592.
8. Sato, S., J. Chem. Phys., 23 (1955) 2465.
9. Murrel, J. N., Carter, S., Farantos, S. C., Huxley, P., Varandas, A. J. C., Molecular Potential Energy Functions. Wiley (1984).
10. Rydberg, R., Z. Phys., 73(1931) 376.
11. Herbst, E., Chem. Phys. Lett., 47 (1977) 517.
12. Varandas, A. J. C., Adv Chem Phys., 74 (1988) 255.
13. Garcia, E., Tese de Doutorado, Universidade do País Basco (1986), E. Garcia e A. Laganà, Mol. Phys., 56 (1985) 621 e Garcia e A. Laganà, Mol. Phys., 56 (1985) 629.
14.  Pauling, L., J Am. Chem. Soc., 69 (1947) 542.
15. Morse, P. N., Phys. Ver., 34 (1929) 57.
16. Herzberg, G., Molecular Spectra and Molecular Structure, II. Electronic Spectra and Electronic Structure of Diatomic Molecules. Van Nostrand, 1979; Huber, K. P. and Herzberg, G., Molecular Spectra and Molecular Structure, IV. Constants of Diatomic Molecules. Van Nostrand 1979.
17. Edgar, T.F., Himmelblau, D.M., Chemical Engineering Series: optimization of chemical process. Boston, Massachusetts. McGrallHill, 1988. Cap 1-4.
18. Kirkpatric, S., Gellat, C. D., Vecchi, M. P., Science, 220 (1983) 671-680.
19. Kirkpatrick, S., J. Stat. Phys., 34 (1984) 975-986.

20. Ceperley, D., Alder, B., Science., 231 (1986) 555.
21. Szu, H., Hartley, R., Phys. Lett., A 122 (1987) 157.
22. Tsallis, C., J. Stat. Phys., 52 (1988) 479.
23. Mundim, K.C. and Tsallis, C., Int. J. Quantum Chem. 58: (4) (1996) 373-381
24. Tsallis, C., Stariolo, D. A., in Annual Reviews of Computational Physics, volII, D. Stauffer. World Scientific, Singapure (1995).
25. Moret, M.A.,  Dissertação de Mestrado: IF-UFBa (Salvador) 1996
26. Morse, P. and Feshbach, H. Methods of Theoretical Physics, McGraw-Hill Book Co. Inc. NY, 1953
27. Jaquet, R., Cencek, W., Rychlewski, J., Kutzelnigg, W.. J. Chem. Phys. 108 (1998) 2831.
28. Jaquet, R., Cencek, W., Rychlewski, J., Kutzelnigg, W.. J. Chem. Phys. 108 (1998) 2837.
29. Soares Neto, J. J., Lindenberg, J.. J. Comp. Chem. 12 (1991) 1237.
30. Tennyson, J., Miller, S.. Comp. Phys. Comm., 55 (1989) 149.